What Is The Necessary And Sufficient Condition For Derivative Existence In F(Z)?
Necessary And Sufficient Conditions
Keywords searched by users: What is the necessary and sufficient conditions for the existence of the derivative of f z )
What Are The Necessary Conditions For Derivative?
Certainly! Here’s a rewritten and expanded paragraph that provides a more comprehensive understanding of the necessary conditions for a derivative to exist:
“In order for a derivative to exist at a specific point on the graph of a function, several conditions must be met. To provide a clearer perspective, let’s delve into these conditions. First, informally, we can think of the graph as being ‘well behaved.’ This means that it should exhibit a continuous, smooth curve at the point in question, with no sudden jumps, sharp corners, or vertical tangents. Imagine you’re tracing the graph with a pen, and there are no interruptions or abrupt changes in direction at that particular spot.
Now, for a more formal explanation, we consider two key criteria: continuity and existence. The derivative exists at a point x = c if and only if two conditions are satisfied. Firstly, the function f must be continuous at x = c. Continuity implies that the function’s values do not experience any sudden breaks or jumps as you approach the point c. In other words, there are no holes or gaps in the graph.
Secondly, the function must simply exist at that point, which means that it has a defined value at x = c. In mathematical terms, there should be a specific y-value associated with the x-coordinate c. These two conditions, continuity and existence, together ensure that the derivative is well-defined and can be calculated at the given point.
So, in summary, for a derivative to exist at a particular point on the graph of a function, both the informal notion of ‘well-behaved’ behavior (smoothness without abrupt changes) and the formal requirements of continuity and existence must be met.”
What Is A Necessary Condition And A Sufficient Condition?
A necessary condition is an essential prerequisite that must be met for an event to take place. It represents a fundamental requirement without which the event cannot occur. In contrast, a sufficient condition refers to a condition or a combination of conditions that, when satisfied, guarantee the occurrence of the event. While a necessary condition is crucial, it is not adequate by itself to trigger the event; additional factors or conditions are usually required to establish a sufficient cause for the event to happen. In summary, necessary conditions are the minimum criteria that need to be fulfilled, while sufficient conditions encompass everything necessary and more to ensure the event’s realization.
What Is Necessary And Sufficient Condition For Differentiability?
What are the essential requirements for a function to be considered differentiable at a specific point? To address this question, let’s delve into the criteria for differentiability. When dealing with a function J that maps from the real plane (IR^2) to the real numbers (IR), it’s crucial to understand that the existence of both partial derivatives at a given point P is a fundamental necessity for differentiability at that point.
Furthermore, research findings from [1], [2], and [3] have shed light on a more nuanced aspect of differentiability. In addition to the necessary condition of having both partial derivatives exist at point P, it has been observed that if one of these partial derivatives is continuous at point P, then the function f is not only necessary but also sufficient for differentiability at that specific point. In other words, continuity of at least one partial derivative, in conjunction with their existence, guarantees the function’s differentiability at point P. This insight adds a layer of depth to our understanding of the conditions required for differentiability in multivariable calculus.
Update 20 What is the necessary and sufficient conditions for the existence of the derivative of f z )




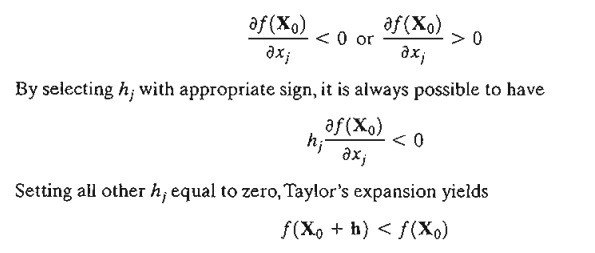
Categories: Aggregate 96 What Is The Necessary And Sufficient Conditions For The Existence Of The Derivative Of F Z )
See more here: trainghiemtienich.com

Learn more about the topic What is the necessary and sufficient conditions for the existence of the derivative of f z ).
- Necessary and sufficient conditions for the existence of a …
- What are the conditions for the existence of the derivative … – Quora
- Confusion of Necessary with a Sufficient Condition
- The Sufficient Condition for the Differentiability of Functions of …
- Primitive function – Encyclopedia of Mathematics
- 2.3 Definition of a derivative – Viewpoint (pwc.com)
See more: https://trainghiemtienich.com/category/travel blog