삼각형의 넓이를 구하는 방법은 여러 가지가 있지만, 그 중에서도 헤론의 공식은 특히 유용하고 매력적인 공식입니다. 특히 삼각형의 세 변의 길이만 알고 있을 때, 높이를 알 수 없는 경우에 매우 유용하게 활용할 수 있습니다.
헤론의 공식은 고대 그리스의 수학자 헤론 (Heron of Alexandria)이 발견한 공식으로, 삼각형의 넓이를 삼각형의 세 변의 길이만으로 구할 수 있는 공식입니다.
헤론의 공식은 무엇일까요?
헤론의 공식은 다음과 같습니다.
“`
S = √(s(s-a)(s-b)(s-c))
“`
여기서:
S는 삼각형의 넓이를 나타냅니다.
a, b, c는 삼각형의 세 변의 길이를 나타냅니다.
s는 삼각형의 반둘레를 나타내며, s = (a + b + c) / 2 로 계산됩니다.
헤론의 공식을 사용하는 방법
헤론의 공식을 사용하여 삼각형의 넓이를 구하는 방법은 다음과 같습니다.
1. 삼각형의 세 변의 길이를 구합니다.
2. 반둘레 (s)를 계산합니다. s = (a + b + c) / 2
3. 헤론의 공식에 값을 대입하여 넓이 (S)를 계산합니다. S = √(s(s-a)(s-b)(s-c))
예시: 헤론의 공식을 사용하여 삼각형의 넓이 구하기
예를 들어, 세 변의 길이가 각각 5cm, 7cm, 8cm인 삼각형의 넓이를 구해 봅시다.
1. 삼각형의 세 변의 길이: a = 5cm, b = 7cm, c = 8cm
2. 반둘레 (s): s = (5 + 7 + 8) / 2 = 10cm
3. 헤론의 공식에 값을 대입: S = √(10(10-5)(10-7)(10-8)) = √(10 * 5 * 3 * 2) = √300 ≈ 17.32 cm²
따라서, 세 변의 길이가 각각 5cm, 7cm, 8cm인 삼각형의 넓이는 약 17.32 cm²입니다.
헤론의 공식의 유용성
헤론의 공식은 다음과 같은 이유로 매우 유용합니다.
삼각형의 높이를 알 필요가 없다: 높이는 삼각형의 넓이를 구하는 데 필요하지만, 헤론의 공식을 사용하면 삼각형의 높이를 알 필요 없이 넓이를 구할 수 있습니다.
세 변의 길이만 알면 된다: 헤론의 공식은 삼각형의 세 변의 길이만 알면 넓이를 구할 수 있는 공식이기 때문에, 삼각형의 다른 정보를 알 필요가 없습니다.
다양한 삼각형에 적용 가능: 헤론의 공식은 모든 종류의 삼각형에 적용할 수 있는 공식입니다.
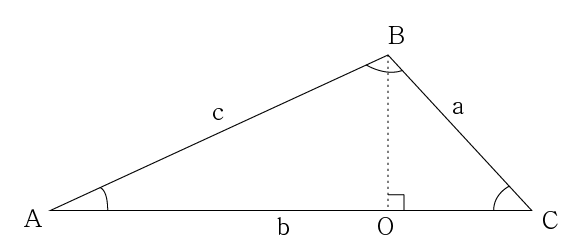
헤론의 공식의 증명
헤론의 공식은 삼각형의 넓이와 관련된 여러 공식을 사용하여 증명할 수 있습니다. 그 중 하나는 코사인 법칙을 사용하는 방법입니다.
1. 코사인 법칙: 삼각형의 한 변의 길이를 다른 두 변의 길이와 그 사이의 각의 코사인 값으로 표현하는 법칙입니다.
2. 삼각형의 넓이 공식: 삼각형의 넓이는 밑변과 높이의 곱의 절반과 같습니다.
3. 삼각형의 넓이를 코사인 법칙을 사용하여 표현합니다.
4. 삼각형의 넓이를 변수 s (반둘레)로 표현합니다.
5. 헤론의 공식을 얻습니다.
헤론의 공식과 관련된 다른 공식
헤론의 공식은 삼각형의 넓이를 구하는 데 유용한 공식이며, 이 공식과 관련하여 몇 가지 다른 공식들이 있습니다.
브라마굽타 공식: 이 공식은 원에 내접하는 사각형의 넓이를 구하는 데 사용됩니다.
브라마굽타-헤론 공식: 이 공식은 원에 내접하는 사다리꼴의 넓이를 구하는 데 사용됩니다.
헤론의 공식의 활용
헤론의 공식은 다양한 분야에서 활용됩니다.
건축: 건물의 면적을 계산하는 데 사용됩니다.
토지 측량: 토지의 면적을 계산하는 데 사용됩니다.
기하학: 삼각형의 넓이를 구하는 데 사용됩니다.
물리: 삼각형의 넓이를 이용하여 물체의 무게 중심을 계산하는 데 사용됩니다.
헤론의 공식: 요약
헤론의 공식은 삼각형의 넓이를 구하는 데 유용한 공식입니다. 특히 삼각형의 높이를 알 수 없는 경우에 매우 유용합니다. 헤론의 공식은 삼각형의 세 변의 길이만 알면 넓이를 구할 수 있기 때문에, 다양한 분야에서 활용됩니다.
헤론의 공식과 관련된 FAQ
Q. 헤론의 공식은 어떻게 유도되었나요?
A. 헤론의 공식은 삼각형의 넓이와 관련된 여러 공식을 사용하여 증명할 수 있습니다. 그 중 하나는 코사인 법칙을 사용하는 방법입니다.
Q. 헤론의 공식은 어떤 삼각형에 적용할 수 있나요?
A. 헤론의 공식은 모든 종류의 삼각형에 적용할 수 있습니다. 직각삼각형, 이등변삼각형, 정삼각형 등 어떤 삼각형이든 세 변의 길이만 알면 넓이를 구할 수 있습니다.
Q. 헤론의 공식을 사용하여 넓이를 구하는 것은 다른 방법보다 더 복잡한가요?
A. 헤론의 공식은 삼각형의 높이를 구할 필요가 없기 때문에, 높이를 알 수 없는 경우에 유용합니다. 하지만, 삼각형의 높이를 알고 있다면, 높이를 이용하여 넓이를 구하는 것이 더 간단할 수 있습니다.
Q. 헤론의 공식은 실제로 어떻게 활용되나요?
A. 헤론의 공식은 다양한 분야에서 활용됩니다. 예를 들어, 건축에서는 건물의 면적을 계산하는 데 사용되고, 토지 측량에서는 토지의 면적을 계산하는 데 사용됩니다.
Q. 헤론의 공식은 어떤 다른 공식과 관련이 있나요?
A. 헤론의 공식은 브라마굽타 공식과 브라마굽타-헤론 공식과 관련이 있습니다. 브라마굽타 공식은 원에 내접하는 사각형의 넓이를 구하는 데 사용되며, 브라마굽타-헤론 공식은 원에 내접하는 사다리꼴의 넓이를 구하는 데 사용됩니다.
헤론의 공식은 삼각형의 넓이를 구하는 데 유용한 공식이며, 이 공식을 이해하면 삼각형과 관련된 다양한 문제를 해결하는 데 도움이 될 것입니다.
헤론의 공식
사용자가 검색하는 키워드: 헤론 의 공식
주제에 관한 이미지 헤론 의 공식

카테고리: 헤론의 공식: 삼각형 넓이를 쉽고 빠르게 계산하는 놀라운 비법!
여기서 더 읽어보세요: trainghiemtienich.com


![[수학1 개념&대표유형] 헤론의 공식 - YouTube [수학1 개념&대표유형] 헤론의 공식 - Youtube](https://i.ytimg.com/vi/-s-fx-KisQ4/maxresdefault.jpg)


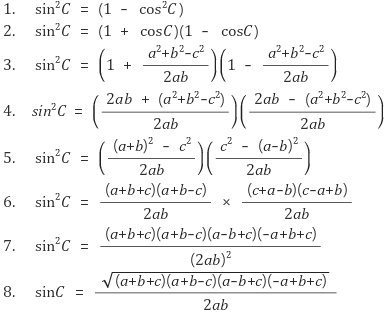




![[다증명] 헤론의 공식 증명 6개중 4번 - 삼각형의 세 변이 주어질 때 넓이 구하는 공식 Heron의 공식 중등수학 중등기하 ... [다증명] 헤론의 공식 증명 6개중 4번 - 삼각형의 세 변이 주어질 때 넓이 구하는 공식 Heron의 공식 중등수학 중등기하 ...](https://i.ytimg.com/vi/xMpHAsQr_hw/maxresdefault.jpg)

![[헤론의 공식] 삼각함수를 이용한 헤론의 공식의 증명 : 네이버 블로그 [헤론의 공식] 삼각함수를 이용한 헤론의 공식의 증명 : 네이버 블로그](http://postfiles9.naver.net/20140120_264/yh6613_1390216008052yhjSg_JPEG/%BB%EF%B0%A2%C7%D4%BC%F6%B8%A6_%C0%CC%BF%EB2.jpg?type=w2)
![[헤론의 공식] 삼각함수를 이용한 헤론의 공식의 증명 : 네이버 블로그 [헤론의 공식] 삼각함수를 이용한 헤론의 공식의 증명 : 네이버 블로그](https://postfiles.pstatic.net/20140214_36/yh6613_1392382021145JYPSE_JPEG/%C7%EC%B7%D0%C0%C7_%B0%F8%BD%C4.jpg?type=w2)
![[헤론의 공식] 오직 세 변의 길이만 주어졌을 때 삼각형의 넓이 구하는 공식 : 네이버 블로그 [헤론의 공식] 오직 세 변의 길이만 주어졌을 때 삼각형의 넓이 구하는 공식 : 네이버 블로그](https://postfiles.pstatic.net/20110810_116/alwaysneoi_1312968292708QcYCa_JPEG/%C7%EC%B7%D0%C0%C7_%B0%F8%BD%C4_%C1%F5%B8%ED.jpg?type=w2)

![[수1] 삼각형의 넓이를 구하는 9가지 방법 : 네이버 블로그 [수1] 삼각형의 넓이를 구하는 9가지 방법 : 네이버 블로그](http://postfiles16.naver.net/MjAxNzA4MThfMjAx/MDAxNTAyOTg5MjU0OTg1.JX1M9yezZpgKx2doQ9YIPZFhZpWlnIOTGY2OD_kUpYcg.jKpX555-SfO9-LbkwS7G62xfT_e8ZhhG4I8KWIX_hl4g.PNG.sm18570/%ED%97%A4%EB%A1%A0%EC%9D%98%EA%B3%B5%EC%8B%9D_%EC%A6%9D%EB%AA%85_2.png?type=w1)


![[수1/기하] 브라마굽타&헤론 공식 - YouTube [수1/기하] 브라마굽타&헤론 공식 - Youtube](https://i.ytimg.com/vi/QZN-UfdkVIk/hq2.jpg?sqp=-oaymwEoCOADEOgC8quKqQMcGADwAQH4AbYIgAKAD4oCDAgAEAEYMiBlKGAwDw==&rs=AOn4CLDyepfDl2xlv7jqq4cBPI8ibUAY-w)

![[수학자이야기] 실용성을 중시한 수학자 헤론, 그는 수학의 이단아? : 네이버 포스트 [수학자이야기] 실용성을 중시한 수학자 헤론, 그는 수학의 이단아? : 네이버 포스트](https://post-phinf.pstatic.net/MjAxOTEyMThfMTEx/MDAxNTc2NjU3Njc2Mjc4.thycWC3jQT7ON0atVwaE_bVUF5_KlLlQxE57qT3H2Gwg.rhejert1DVdSoMuWm2sf1dvDz99o8W9m-ecFATPQ-J4g.JPEG/1%EC%9B%94_%EC%88%98%ED%95%99%EC%9E%90_%EB%B8%94%EB%A1%9C%EA%B7%B8%EC%9A%A9_%ED%97%A4%EB%A1%A0.jpg?type=w1200)
![[헤론의공식!] 왜요? 공식만 암기? ️ 헤롱 아니고,헤론 - YouTube [헤론의공식!] 왜요? 공식만 암기? ️ 헤롱 아니고,헤론 - Youtube](https://i.ytimg.com/vi/xpYWwW2pVGA/hqdefault.jpg)



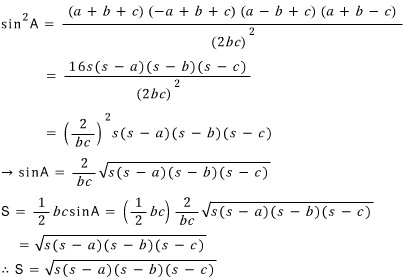







![[수1] 세변의 길이가 주어졌을때 삼각형 넓이 구하기!1.헤론공식 2.코사인 법칙을 이용한 사인법칙이용! [고2] 기말고사 ... [수1] 세변의 길이가 주어졌을때 삼각형 넓이 구하기!1.헤론공식 2.코사인 법칙을 이용한 사인법칙이용! [고2] 기말고사 ...](https://i.ytimg.com/vi/2CpmrvQa1LA/hqdefault.jpg)
![삼각형의 넓이 구하기 (feat. 헤론의 공식, 신발끈 공식) [이투스 한컷강의 수학 한정윤 선생님] - YouTube 삼각형의 넓이 구하기 (Feat. 헤론의 공식, 신발끈 공식) [이투스 한컷강의 수학 한정윤 선생님] - Youtube](https://i.ytimg.com/vi/h96CkYOnjLQ/maxresdefault.jpg)





![[가/나] 21수능을 위한 기하학 공식들 - 오르비 [가/나] 21수능을 위한 기하학 공식들 - 오르비](https://s3.orbi.kr/data/file/united2/9e2ede9c-5a82-4ef0-ae8a-982bb2c3b0a8.png)







![[중3] 원에 내접하는 사각형의 성질 - YouTube [중3] 원에 내접하는 사각형의 성질 - Youtube](https://i.ytimg.com/vi/Yj6650YXpf0/maxresdefault.jpg)

![[数1]ヘロンの公式の使い方と計算方法、注意点 | 数学のトムラボ [数1]ヘロンの公式の使い方と計算方法、注意点 | 数学のトムラボ](https://rikeinvest.com/wp-content/uploads/%E3%83%98%E3%83%AD%E3%83%B3%E3%81%AE%E5%85%AC%E5%BC%8F%E3%82%B5%E3%83%A0%E3%83%8D-1.webp)










![[중3-2 꿀팁강의] 삼각비 #10탄 || 삼각형의 높이 구하기 (예각, 둔각이 주어진 경우) - YouTube [중3-2 꿀팁강의] 삼각비 #10탄 || 삼각형의 높이 구하기 (예각, 둔각이 주어진 경우) - Youtube](https://i.ytimg.com/vi/9WPwoD73tUQ/maxresdefault.jpg)



![[다람지아] 헤론 일렉트릭헤론 적목귀 - 신비아파트 고스트헌터 게임 - YouTube [다람지아] 헤론 일렉트릭헤론 적목귀 - 신비아파트 고스트헌터 게임 - Youtube](https://i.ytimg.com/vi/2XCED3UU8OM/hqdefault.jpg)
이 기사에 대한 링크: 헤론 의 공식.
자세한 내용은 이 항목을 참조하세요: 헤론 의 공식.
- 1. 헤론의 공식 유도 (A derivation of Heron’s formula)
- 헤론의 공식
- 헤론 공식 – 위키백과, 우리 모두의 백과사전
- 헤론의 공식, 헤론의 공식 유도
- 007. 헤론의 공식 – 네이버 블로그
- [IMATH] 헤론의 공식과 그 증명
여기서 더 보기: https://trainghiemtienich.com/category/religion blog