라그랑주 정리
라그랑주 정리는 영국의 수학자 라그랑주(Joseph-Louis Lagrange)가 발견한 중요한 수학적 원리로, 함수의 극값을 찾는 문제를 해결하는 데 사용됩니다. 이 정리는 최대값과 최소값을 찾는 최적화 문제에 널리 응용되며, 미분법과 선형대수학의 기본 개념들을 이해하는 데 중요한 역할을 합니다.
1. 라그랑주 정리란?
라그랑주 정리는 한정 조건(constraints)하에서 함수의 극값을 찾는 문제를 해결하기 위해 사용됩니다. 이 정리는 함수가 미분 가능하고, 한정 조건이 선형적이고 연속적일 때 유효합니다. 라그랑주 정리는 원래 18세기에 개발되었지만, 현대적인 의미로 널리 사용되는 것은 19세기 후반 이후입니다.
2. 라그랑주 정리의 역사적 배경
라그랑주 정리는 1762년에 처음 발견되었으며, 라그랑주가 1773년에 발표한 “목록에 포함된 해설과 이미 검증된 예제들의 적응”이라는 책에서 정식으로 증명되었습니다. 이 책은 라그랑주의 수학적 인사이트와 문제 해결 능력을 보여주며, 그의 수학적 업적의 중요한 부분입니다.
3. 라그랑주 정리의 수학적 원리와 증명
라그랑주 정리는 함수의 극값을 찾는 최적화 문제에 적용되는 원리입니다. 이 원리에 의하면, 함수 f가 함수 g에 대한 일정한 한정 조건 하에서 극값을 갖는다면, 이 극값은 라그랑주 승수법(Lagrange multiplier method)을 사용하여 찾을 수 있습니다. 라그랑주 승수는 한정 조건에 적절한 가중치를 부여하여 극값을 찾기 위해 사용되는 변수입니다.
라그랑주 정리의 증명은 복잡하지만, 주로 라그랑주 승수법을 사용하여 이루어집니다. 라그랑주 항등식 증명을 통해 한정 조건을 만족하는 점에서 함수의 접선 방향을 고려하고, 라그랑주 승수를 도입하여 극값을 찾을 수 있습니다.
4. 라그랑주 정리의 응용 분야
라그랑주 정리는 다양한 분야에 응용되며, 특히 경제학, 물리학, 공학, 운송과학 등에서 사용됩니다. 이런 응용 분야에서는 종종 최적화 문제를 해결해야 하며, 라그랑주 정리를 사용하여 이러한 문제를 해결할 수 있습니다. 예를 들어, 경제학에서는 소비자의 효용 최대화 또는 생산자의 이윤 최대화를 위해 최적화 문제를 다루며, 이때 라그랑주 정리를 활용합니다.
5. 라그랑주 정리와 최적화 문제
라그랑주 정리는 최적화 문제를 해결하는 데 가장 널리 사용되는 도구 중 하나입니다. 최적화 문제란, 주어진 조건을 만족하면서 목적 함수의 값을 최대 또는 최소로 만드는 문제입니다. 라그랑주 정리는 이러한 문제를 해결하는 도구로서, 한정 조건 아래에서의 극값을 찾는 데 사용됩니다.
6. 라그랑주 승수법과 라그랑주 이득함수
라그랑주 승수법은 라그랑주 정리를 증명하고 최적화 문제를 해결하기 위해 사용되는 기법입니다. 라그랑주 승수법은 기존의 목적 함수에 한정 조건을 고려한 라그랑주 항등식을 추가하는 방식으로 동작합니다. 이를 통해 최적화 문제를 라그랑주 승수법을 사용하여 푸는 데 사용되는 라그랑주 이득함수를 도출할 수 있습니다.
7. 라그랑주 정리의 한계와 극복 방법
라그랑주 정리는 미분 가능하고 선형적인 한정 조건을 갖는 경우에만 유용하게 사용될 수 있습니다. 이러한 제한으로 인해 일부 문제에는 적용하기 어려울 수 있습니다. 또한, 라그랑주 정리는 최적화 문제를 푸는 데에만 사용되며, 함수의 해석적인 형태를 제시하지 않습니다.
라그랑주 정리의 한계를 극복하기 위해 다른 최적화 알고리즘과 기법들이 개발되었습니다. 이러한 알고리즘은 보다 더 일반적인 문제에 유용하며, 라그랑주 정리와 함께 사용될 때 효과적인 최적화 문제 해결의 도구가 될 수 있습니다.
8. 라그랑주 정리의 현대적 의미와 중요성
라그랑주 정리는 최적화 문제를 해결하기 위한 중요한 도구로서, 다양한 수학적, 과학적 응용 분야에서 활용됩니다. 이 정리는 선형대수학과 미적분학의 기본 원리들과 깊은 관련이 있으며, 수학적 인사이트와 증명의 복잡성으로 인해 현대적인 의미와 중요성을 가집니다.
이러한 의미에서, 라그랑주 정리는 최적화 문제 해결에 필수적인 도구로서 많은 수학자와 과학자에게 큰 영감을 주고 있으며, 다양한 분야에서의 연구와 응용에 영향을 미치고 있습니다.
FAQs:
Q: 라그랑주 정리는 어떤 문제를 해결하려고 사용될까요?
A: 라그랑주 정리는 주어진 조건 하에서 함수의 극값을 찾는 최적화 문제를 해결하는 도구로 사용됩니다.
Q: 라그랑주 정리의 증명은 어려운가요?
A: 라그랑주 정리의 증명은 복잡하지만, 주로 라그랑주 승수법을 사용하여 이루어집니다.
Q: 라그랑주 정리는 어떤 분야에서 응용되나요?
A: 라그랑주 정리는 경제학, 물리학, 공학, 운송과학 등 다양한 분야에서 응용되며, 최적화 문제를 해결하는 데 사용됩니다.
Q: 라그랑주 승수법이 무엇인가요?
A: 라그랑주 승수법은 라그랑주 정리를 증명하고 최적화 문제를 해결하기 위해 사용되는 기법으로, 한정 조건을 고려한 라그랑주 항등식을 추가하는 방식으로 동작합니다.
Q: 라그랑주 정리의 한계는 무엇인가요?
A: 라그랑주 정리는 미분 가능하고 선형적인 한정 조건을 갖는 경우에만 사용될 수 있으며, 일부 문제에는 적용하기 어려울 수 있습니다.
사용자가 검색한 키워드: 라그랑주 정리 라그랑주 방정식, 라그랑주 네 제곱수 정리, 라그랑주 승수법, 라그랑주 포인트, 라그랑주 점, 라그랑주 항등식 증명, 라그랑주 역학, 라그랑주 완화 법
Categories: Top 99 라그랑주 정리
현대대수학 10절 4: 라그랑지 정리, 지수
여기에서 자세히 보기: trainghiemtienich.com
라그랑주 방정식
라그랑주 방정식은 18세기 프랑스 수학자인 조셉 라그랑주(Joseph-Louis Lagrange)가 개발했습니다. 이 방정식은 조건부 최적화 문제에서 주어진 조건 하에서 함수의 극소 또는 극대 값을 찾는 데 사용됩니다. 이때 조건은 등식 또는 부등식 형태로 주어질 수 있습니다. 예를 들어, 물건을 생산하는 회사에서 생산 비용을 최소화하는 문제나, 힘의 크기와 방향이 주어진 상태에서 힘의 작용 지점을 결정하는 문제 등이 라그랑주 방정식으로 해결될 수 있습니다.
라그랑주 방정식은 주어진 조건을 고려하여 목적 함수와 제한 조건을 결합하는 방식으로 구성됩니다. 이때 목적 함수는 최소화 또는 최대화하려는 함수로 정의되며, 제한 조건은 동시에 만족되어야 하는 조건입니다. 이를 수식으로 표현하면 다음과 같습니다.
L(x, λ) = f(x) + λg(x)
여기서 L은 라그랑주 함수(Lagrange function)를 나타내며, x는 변수, λ는 라그랑주 승수(Lagrange multiplier)입니다. f(x)는 최적화하려는 목적 함수를, g(x)는 제한 조건을 나타냅니다. 라그랑주 방정식에서 우리의 목표는 이 함수 L을 최소 또는 최대화하는 x와 λ를 찾는 것입니다.
라그랑주 방정식을 푸는 방법은 크게 두 가지로 나뉩니다. 첫 번째는 L 함수를 변수 x에 대해 편미분한 식을 0으로 놓고, 이를 x에 대해 해결하는 것입니다. 두 번째는 g(x)가 등식인 경우 L을 변수 λ에 대해 편미분한 식을 0으로 놓고, 이를 λ에 대해 해결한 후, 다시 g(x)에 대입하여 실제 변수 x를 찾는 것입니다.
라그랑주 방정식에는 몇 가지 중요한 개념이 있습니다. 첫 번째로, 라그랑주 승수인 λ는 제한 조건을 만족시키기 위한 가중치 역할을 합니다. 즉, λ는 제한 조건에 대한 민감도를 나타냅니다. 라그랑주 승수가 양수일 경우, 제한 조건을 적극적으로 반영하는 것을 의미합니다. 두 번째로, 등식인 제한 조건이 주어지는 경우에는 라그랑주 방정식으로 문제를 해결할 수 있습니다. 하지만 부등식인 제한 조건이 주어진다면, 슬랙 조건(slack condition)이 추가로 고려되어야 합니다.
라그랑주 방정식을 사용하는 몇 가지 예시를 살펴보겠습니다. 첫 번째로, 점과 직선 사이의 최단 거리를 구하는 문제를 생각해봅시다. 점 P(x, y)와 직선 ax + by + c = 0 사이의 거리는 d = |ax + by + c| / √(a^2 + b^2)로 나타낼 수 있습니다. 이때 최단 거리를 구하는 문제는 최적화 문제로 볼 수 있으며, 라그랑주 방정식을 사용하여 해결할 수 있습니다.
두 번째 예시로, 생산 비용을 최소화하는 문제를 생각해봅시다. 회사가 생산하는 제품의 제한된 자원이 주어졌을 때, 생산 비용을 최소화하는 최적의 생산량을 찾는 문제입니다. 이때 제한된 자원에 대한 조건을 고려할 수 있도록 라그랑주 방정식을 사용할 수 있습니다.
FAQs:
Q: 라그랑주 방정식은 어떤 분야에서 주로 활용될까요?
A: 라그랑주 방정식은 물리학, 공학, 경제학, 운영 연구 등 다양한 분야에서 사용됩니다. 다양한 제한 조건이 있는 최적화 문제를 해결하는 경우 라그랑주 방정식을 활용할 수 있습니다.
Q: 라그랑주 방정식을 해결하는 과정이 어렵지 않을까요?
A: 라그랑주 방정식은 특정 문제에 대해 명확한 수식을 도출할 수 있다면 상대적으로 간단한 방법입니다. 하지만 문제에 따라 복잡한 계산이 요구될 수 있으므로, 직관적인 이해와 연습이 필요합니다.
Q: 라그랑주 승수는 어떤 의미를 가지나요?
A: 라그랑주 승수는 제한 조건을 만족시키기 위한 가중치 역할을 합니다. 제한 조건에 대한 민감도를 나타내며, 승수의 값에 따라 제한 조건이 얼마나 반영되는지 결정됩니다.
Q: 라그랑주 방정식은 부등식 제한 조건에도 사용할 수 있나요?
A: 라그랑주 방정식은 등식인 제한 조건에 대해 주로 사용됩니다. 하지만 부등식인 제한 조건이 주어질 경우, 슬랙 조건을 추가로 고려해야 합니다.
Q: 라그랑주 방정식을 사용한 예시를 더 알려주세요.
A: 라그랑주 방정식은 최단 거리 문제, 최적 생산 비용 문제, 최대 소득 문제 등 다양한 최적화 문제에 적용될 수 있습니다. 이 방정식은 제한 조건이 있는 문제를 해결하는 데에 유용하게 사용됩니다.
라그랑주 네 제곱수 정리
라그랑주 네 제곱수 정리(Lagrange’s Four Square Theorem)는 어떤 자연수를 정확히 네 개의 제곱수의 합으로 나타낼 수 있는지에 대한 정리이다. 이 정리는 1770년에 프랑스 수학자 조제프 라그랑주(Joseph-Louis Lagrange)에 의해 처음으로 증명되었으며, 그렇기 때문에 이러한 이름이 붙여졌다. 이 정리는 수학에서 매우 중요하고 유용한 결과 중 하나로 꼽히며, 다양한 분야에서 응용될 수 있다.
라그랑주 네 제곱수 정리에 따르면, 어떤 자연수든지 정확히 네 개의 제곱수(a^2, b^2, c^2, d^2)의 합으로 나타낼 수 있다. 즉, 어떤 자연수 n에 대해서 다음과 같은 식을 만족하는 자연수 a, b, c, d가 있다는 것이다.
n = a^2 + b^2 + c^2 + d^2
라그랑주 네 제곱수 정리는 그 증명이 비교적 간단하면서도 혁신적인 방식으로 이루어진다. 주된 아이디어는 피타고라스 정리(Pythagorean theorem)와 관련이 있다. 피타고라스 정리는 직각 삼각형에서 빗변의 제곱과 다른 두 변의 제곱의 합이 같다는 정리이다. 라그랑주는 이 정리를 이용하여 네 제곱수의 합을 구성하는 방법을 찾았다.
정수를 네 개의 제곱수의 합으로 나타내는 알고리즘은 라그랑주의 방법을 따라 구성될 수 있다. 예를 들어, 41을 네 개의 제곱수의 합으로 나타내려면 다음과 같은 계산을 할 수 있다.
41 = 4^2 + 4^2 + 4^2 + 3^2
라그랑주 네 제곱수 정리는 대표적인 예로 피타고라스 정리를 생각해볼 수 있다. 피타고라스 정리는 어떤 자연수 n이 삼각형의 변의 길이로 나타낼 수 있는지 알려주는 정리이다. 라그랑주 네 제곱수 정리도 자연수 n을 네 개의 제곱수의 합으로 나타낼 수 있는지 알려준다는 점에서 비슷하다. 또한, 라그랑주 네 제곱수 정리는 어떤 자연수도 정확히 네 개의 제곱수의 합으로 나타낼 수 있다는 점에서 더 확장된 개념이다.
라그랑주의 네 제곱수 정리는 수학에서 다양한 분야에서 응용될 수 있다. 예를 들어, 네 제곱수 정리는 분수 표현의 연구에서 큰 역할을 한다. 분수 표현은 대략적인 값을 정확히 표현하는 데 사용되는데, 네 제곱수의 합을 이용하여 다양한 분수를 정확히 표현할 수 있다. 또한, 네 제곱수 정리는 해석학에서 빛을 발할 수 있는데, 확률론과 조합론에서 사용되는 것을 볼 수 있다.
라그랑주 네 제곱수 정리에 대한 자주 묻는 질문들(FAQs)
Q: 라그랑주 네 제곱수 정리는 어떻게 증명되었나요?
A: 라그랑주는 피타고라스 정리와 다른 방식의 증명을 통해 이 정리를 증명했습니다. 그의 증명은 혁신적이면서도 간단한 방법으로 구성되었습니다.
Q: 라그랑주 네 제곱수 정리는 어떻게 활용될 수 있나요?
A: 네 제곱수 정리는 분수 표현, 해석학, 통계학 등 다양한 분야에서 응용될 수 있습니다. 예를 들어, 분수 표현에서 정확한 값을 표현하는 데 사용되며, 해석학에서 확률론과 조합론과 연관되어 사용될 수 있습니다.
Q: 네 제곱수 정리에 대한 다른 유명한 예는 무엇이 있나요?
A: 피타고라스 정리는 가장 잘 알려진 네 제곱수 정리의 예입니다. 피타고라스 정리는 직각 삼각형의 변의 길이를 나타내는 구식입니다.
Q: 어떤 자연수는 네 개 이상의 제곱수의 합으로 나타낼 수 있을까요?
A: 라그랑주 네 제곱수 정리는 자연수를 정확히 네 개의 제곱수의 합으로 나타낼 수 있는 것을 보장해줍니다. 따라서 네 개 이상의 제곱수의 합으로 나타내는 것은 불가능합니다.
Q: 네 제곱수 정리와 관련된 다른 중요한 정리나 개념은 무엇이 있나요?
A: 네 제곱수 정리와 관련된 중요한 개념으로 피타고라스 정리와 페르마의 마지막 정리가 있습니다. 피타고라스 정리는 삼각형에서 변의 길이를 나타내는 정리이며, 페르마의 마지막 정리는 a^n + b^n = c^n의 형태의 방정식을 만족하는 자연수 해가 존재하지 않는다는 것을 증명한 정리입니다.
주제와 관련된 이미지 라그랑주 정리

라그랑주 정리 주제와 관련된 이미지 43개를 찾았습니다.


![유니스터디] 권준표 교수님의 제대로 끝내는 동역학 강의🔖4강_확장 해밀턴 원리, 오일러 라그랑주 방정식(Euler-Lagrangian) 개념 정리) - YouTube 유니스터디] 권준표 교수님의 제대로 끝내는 동역학 강의🔖4강_확장 해밀턴 원리, 오일러 라그랑주 방정식(Euler-Lagrangian) 개념 정리) - Youtube](https://i.ytimg.com/vi/7cymhJUihVY/maxresdefault.jpg)
![미적분학] 13.8 라그랑주 승수 (Part2. 예제 2~4) - YouTube 미적분학] 13.8 라그랑주 승수 (Part2. 예제 2~4) - Youtube](https://i.ytimg.com/vi/wv7wXqCmauY/maxresdefault.jpg)


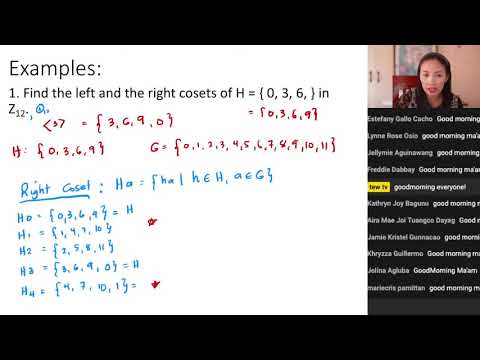


Article link: 라그랑주 정리.
주제에 대해 자세히 알아보기 라그랑주 정리.