사다리꼴 둘레 공식: 수학의 신비를 풀다
사다리꼴 넓이 구하는 8가지 방법
Keywords searched by users: 사다리꼴 둘레 공식 삼각형 둘레 공식, 사각형의 둘레 공식, 사다리꼴 넓이 공식, 정삼각형 둘레 공식, 평행사변형 둘레 공식, 도형의 둘레 공식, 직사각형 둘레 공식, 도형의 둘레 공식 모음
사다리꼴 둘레 공식: 깊이 이해하고 정확히 계산하기
1. 사다리꼴 둘레의 개념
사다리꼴은 네 변 중 두 변이 평행하고 나머지 두 변이 평행하지 않은 도형입니다. 이 도형의 둘레를 계산하는 사다리꼴 둘레 공식은 기본적인 수학 개념 중 하나입니다. 둘레는 도형의 주요 특성 중 하나로, 이를 정확히 계산하기 위해 몇 가지 핵심 개념을 이해해야 합니다.
2. 사다리꼴 둘레 공식의 기본 구성 요소
사다리꼴 둘레를 계산하는 데 필요한 주요 구성 요소는 두 변의 길이와 대각선의 길이입니다. 이를 각각 a, b, c라고 하겠습니다. 여기서 a와 b는 평행한 두 변이고, c는 두 변을 연결하는 대각선입니다. 이러한 변수를 사용하여 사다리꼴 둘레를 계산할 수 있습니다.
3. 사다리꼴 둘레 공식의 유도
사다리꼴 둘레 공식은 두 변의 길이와 대각선의 길이를 조합하여 얻을 수 있습니다. 이 공식은 다음과 같습니다:
P=a+b+2c
여기서 P는 사다리꼴의 둘레를 나타냅니다. 이 공식은 두 평행한 변의 길이를 더하고, 그 결과에 대각선의 길이를 두 번 더한 값입니다.
4. 사다리꼴 둘레 공식의 예시와 응용
이제 구체적인 예시를 통해 사다리꼴 둘레 공식을 실제로 사용하는 방법을 살펴보겠습니다. 가령, 한 사다리꼴의 평행한 변의 길이가 8cm와 12cm이며, 대각선의 길이가 10cm라고 가정해 봅시다. 이를 공식에 대입하면:
P=8+12+2×10
P=8+12+20
P=40
따라서 이 사다리꼴의 둘레는 40cm입니다. 이러한 예시를 통해 공식을 사용하여 간단하게 둘레를 계산할 수 있습니다.
5. 사다리꼴 둘레 계산의 단계별 안내
둘레를 계산하기 위해서는 몇 가지 단계를 따라가야 합니다. 아래는 각 단계의 세부적인 설명과 함께 예제를 제시한 것입니다:
- 주어진 사다리꼴의 변의 길이와 대각선의 길이 확인
- 공식에 주어진 값 대입: \( P = a + b + 2c \)
- 값 계산 및 결과 도출
예를 들어, a=8, b=12, c=10인 사다리꼴의 둘레를 계산한다면 위의 예시와 같은 방식으로 간단히 해결할 수 있습니다.
6. 주요 오류 및 흔한 오해
둘레를 계산할 때 흔히 발생하는 오류와 오해에 대한 주의사항이 있습니다. 이를 피하기 위해 몇 가지 중요한 지침을 제시하겠습니다:
- 변의 길이를 정확하게 측정하고 대각선의 길이를 정확히 확인해야 합니다.
- 계산 중에 단위를 혼동하지 않도록 주의해야 합니다.
- 공식을 정확하게 이해하고 사용하는 것이 중요합니다. 공식의 각 변수가 무엇을 의미하는지 이해하는 것이 필수적입니다.
7. 사다리꼴 둘레 계산을 위한 도구 및 자원
둘레를 정확하게 계산하기 위해 다양한 도구와 온라인 자원을 활용할 수 있습니다. 아래는 유용한 자원들입니다:
8. 더 나아가기: 고급 둘레 계산 및 응용
둘레 계산에 익숙해진다면 고급 수준의 둘레 계산과 응용에 도전해 볼 수 있습니다. 다양한 도형에 대한 둘레 공식을 습득하고 실제 문제에 적용해 보세요. 아래는 다양한 도형의 둘레 공식 모음입니다:
- 삼각형 둘레 공식
- 사각형의 둘레 공식
- 사다리꼴 넓이 공식
- 정삼각형 둘레 공식
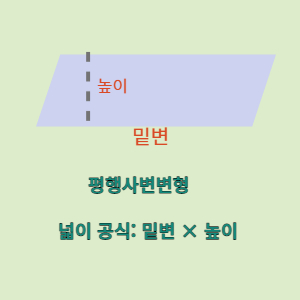
- 평행사변형 둘레 공식
- 도형의 둘레 공식
- 직사각형 둘레 공식
이러한 다양한 도형에 대한 둘레 공식을 숙지하면 더 다양한 수학적 문제를 해결할 수 있을 것입니다.
FAQs (자주 묻는 질문)
Q: 둘레를 계산하는 데 가장 흔한 오류는 무엇인가요?
A: 가장 흔한 오류 중 하나는 변의 길이나 대각선의 길이를 정확하게 측정하지 않는 것입니다. 정확한 값을 사용해야 올바른 결과를 얻을 수 있습니다.
Q: 둘레 공식을 이해하기 어려운데 도움이 될만한 자료가 있나요?
A: 네, Khan Academy의 둘레에 대한 리뷰 자료가 도움이 될 수 있습니다. 해당 자료에서 기본적인 둘레 개념을 다시 학습할 수 있습니다.
Q: 둘레 계산에 사용할 수 있는 온라인 도구가 있을까요?
A: 네, Calculat.org에서는 사다리꼴 둘레를 계산하는데 도움이 되는 온라인 도구를 제공하고 있습니다. 이를 활용하여 빠르게 계산할 수 있습니다.
이 글을 통해 사다리꼴 둘레 공식에 대한 깊은 이해를 얻고, 다양한 도형의 둘레를 계산하는 방법에 대해 학습하였습니다. 정확한 계산을 위해 항상 주어진 값을 정확하게 확인하고, 공식을 올바르게 이해하는 것이 중요합니다. 더 나아가서 다양한 도형에 대한 수학적 지식을 활용하여 다양한 문제를 해결할 수 있기를 바랍니다.
Categories: 공유 16 사다리꼴 둘레 공식

삼각형 둘레 공식
삼각형 둘레 공식: 깊게 파헤치는 안내서
삼각형은 기하학에서 중요한 도형 중 하나로, 다양한 형태와 특성을 가지고 있습니다. 삼각형의 특정한 특성 중 하나는 둘레를 구하는 것인데, 이를 위해 사용되는 삼각형 둘레 공식에 대해 자세히 살펴보겠습니다. 이 문서는 초급자부터 고급 사용자까지 모두에게 유익한 정보를 제공할 것입니다.
삼각형 둘레 공식이란?
삼각형의 둘레를 구하는 공식은 주어진 삼각형의 변들을 활용하여 둘레를 계산하는 방법입니다. 삼각형은 세 개의 변으로 이루어져 있으며, 이 변의 길이를 알고 있으면 삼각형의 둘레를 손쉽게 구할 수 있습니다.
삼각형 둘레 공식은 주로 다음과 같이 표현됩니다.
둘레=a+b+c
여기서 a, b, c는 삼각형의 세 변의 길이를 나타냅니다. 이 공식은 모든 종류의 삼각형에 적용되며, 간단하면서도 효과적인 방법으로 삼각형의 둘레를 계산할 수 있습니다.
삼각형 둘레 공식의 원리
삼각형 둘레 공식의 원리를 이해하기 위해서는 삼각형의 구성과 변의 특성을 고려해야 합니다. 삼각형은 세 변으로 이루어져 있으며, 각 변은 서로 다른 길이를 가지고 있습니다.
삼각형의 둘레는 각 변의 길이를 모두 합한 값으로 정의됩니다. 이는 간단한 논리로 이해할 수 있습니다. 삼각형의 한 꼭지점에서 출발하여 주어진 변을 따라 이동하면서 삼각형의 모든 변을 거치게 됩니다. 이때, 각 변의 길이를 더하면 전체 삼각형의 둘레가 됩니다.
삼각형 둘레 공식의 활용
삼각형 둘레 공식은 다양한 상황에서 유용하게 활용됩니다. 주어진 삼각형의 변의 길이를 알고 있다면, 다음과 같은 상황에서 이 공식을 적용할 수 있습니다.
1. 도형의 둘레 계산
가장 기본적인 용도로, 삼각형의 둘레를 계산하는 데 활용됩니다. 이는 다양한 수학 문제나 현실적인 상황에서 도형의 둘레를 구해야 할 때 사용됩니다.
2. 주어진 변의 길이를 활용한 문제 해결
주어진 삼각형의 변의 길이를 활용하여 다른 속성이나 문제를 해결하는 데에도 적용됩니다. 예를 들어, 삼각형의 넓이를 구하는 문제에서 둘레를 활용할 수 있습니다.
FAQ
1. 삼각형 둘레 공식은 모든 종류의 삼각형에 적용되나요?
네, 삼각형 둘레 공식은 모든 종류의 삼각형에 적용 가능합니다. 정삼각형, 이등변삼각형, 부등변삼각형 등 모든 종류의 삼각형에서 세 변의 길이를 더하여 둘레를 구할 수 있습니다.
2. 삼각형 둘레 공식을 사용할 때 주의할 점은 무엇인가요?
삼각형 둘레 공식을 사용할 때는 주어진 변의 길이를 정확히 파악해야 합니다. 부주의한 계산이나 잘못된 변의 길이 입력은 잘못된 결과를 가져올 수 있습니다.
3. 삼각형 둘레 공식 이외에 다른 관련된 공식이 있나요?
네, 삼각형의 다양한 특성을 나타내는 여러 가지 공식이 존재합니다. 예를 들어, 삼각형의 넓이를 계산하는 공식, 삼각비와 관련된 공식 등이 있습니다.
이 안내서를 통해 삼각형 둘레 공식에 대한 이해를 높이고, 다양한 문제 상황에서 유연하게 활용할 수 있을 것입니다. 삼각형의 다양한 특성을 탐험하고 이를 수학적으로 이해함으로써 수학적 사고 능력을 향상시킬 수 있습니다.
사각형의 둘레 공식
사각형의 둘레 공식: 개념, 계산, 및 자주 묻는 질문
소개
사각형은 기하학에서 중요한 도형 중 하나이며, 이에 관한 수학적인 개념은 다양하게 다뤄집니다. 이 중에서도 사각형의 둘레를 구하는 공식은 매우 기초적이면서도 중요한 개념 중 하나입니다. “사각형의 둘레 공식”은 사각형 주변을 둘러싼 길이를 계산하는 방법을 제시합니다.
사각형의 둘레 공식
사각형의 둘레를 구하는 공식은 간단하게 다음과 같이 표현됩니다:
둘레=2×(가로 길이+세로 길이)
이 공식에서 “가로 길이”는 사각형의 가로 방향 변의 길이를 나타내며, “세로 길이”는 세로 방향 변의 길이를 나타냅니다. 이를 이용하면 어떤 크기의 사각형이든 간단하게 둘레를 구할 수 있습니다.
상세 설명
가로 길이와 세로 길이 이해하기
먼저, 가로와 세로 길이에 대한 이해가 필요합니다. 가로 길이는 사각형의 가로 방향 변이며, 세로 길이는 사각형의 세로 방향 변입니다. 이 두 길이를 알고 있다면, 둘레를 구하는 것은 매우 간단합니다.
공식의 유도
둘레를 구하는 공식은 사실 두 가로 변과 두 세로 변의 길이를 합한 후, 그 값에 2를 곱하는 것입니다. 이는 각 변을 두 번씩 더하는 것과 동일하며, 이로써 주어진 사각형의 둘레를 얻을 수 있습니다.
예시
예를 들어, 가로 길이가 5이고 세로 길이가 3인 사각형의 둘레를 구한다면 다음과 같이 계산할 수 있습니다:
둘레=2×(5+3)=2×8=16
따라서 이 사각형의 둘레는 16입니다.
자주 묻는 질문
1. 둘레 공식 외에 다른 방법이 있을까요?
일반적으로 사각형의 둘레를 구하는 데에는 위에서 설명한 공식이 가장 효과적입니다. 그러나 사실 둘레를 직접 계산하는 것 외에도, 변의 길이를 통해 둘레를 구하는 방법이 있습니다.
2. 사각형의 둘레를 알면 넓이를 어떻게 구할 수 있을까요?
사각형의 둘레만으로는 넓이를 직접적으로 구할 수 없습니다. 넓이를 구하려면 사각형의 가로와 세로 길이를 알아야 합니다. 넓이를 구하는 공식은 다음과 같습니다:
넓이=가로 길이×세로 길이
3. 둘레 공식은 다른 다각형에도 적용될까요?
둘레 공식은 주어진 도형의 변에 따라 다르게 적용됩니다. 사각형의 경우에는 간단하게 주어진 공식을 사용할 수 있지만, 삼각형이나 원과 같은 다른 도형에는 다른 둘레를 구하는 방법이 존재합니다.
4. 왜 둘레를 구하는 것이 중요한가요?
도형의 둘레를 구하는 것은 주어진 형태의 경계 길이를 알아내는 데에 도움을 줍니다. 이는 건축, 디자인, 공학 등 다양한 분야에서 중요한 역할을 합니다.
결론
사각형의 둘레 공식은 간단하지만 중요한 수학적 개념 중 하나입니다. 이를 통해 어떤 크기의 사각형이든 둘레를 효과적으로 계산할 수 있습니다. 이러한 기초적인 지식은 다양한 분야에서 응용될 수 있으며, 수학적 사고력을 향상시키는 데에도 도움이 됩니다.
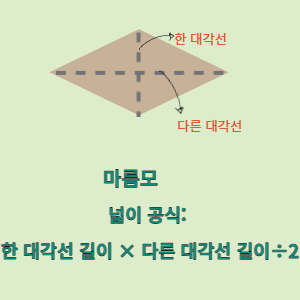
사다리꼴 넓이 공식
사다리꼴 넓이 공식: 깊이 파고들어 설명하는 가이드
사다리꼴은 수학에서 자주 등장하는 도형 중 하나로, 넓이를 구하는 공식은 중요한 수학 개념 중 하나입니다. 이 글에서는 사다리꼴 넓이 공식에 대해 자세하게 다루어보겠습니다. 이 가이드는 초보자부터 중급 수준까지의 독자들을 위해 구성되어 있으며, 주요 개념과 원리를 명확하게 설명할 것입니다.
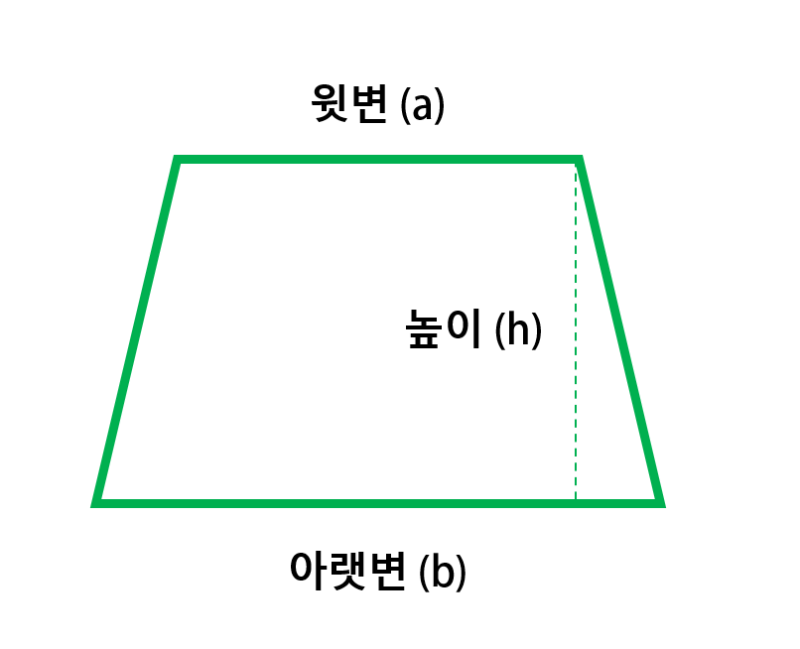
사다리꼴의 정의
먼저, 사다리꼴이 정확히 무엇인지 이해하는 것이 중요합니다. 사다리꼴은 두 개의 평행한 변을 가지고 있는 다각형으로, 대표적으로 윗변과 아랫변이 서로 다른 길이를 가지고 있습니다. 이 두 변이 평행하다는 특징은 사다리꼴을 다른 도형과 구별하는 중요한 특징 중 하나입니다.
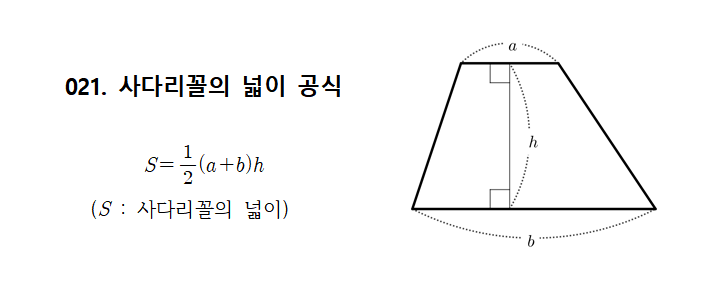
사다리꼴 넓이 공식
사다리꼴의 넓이를 계산하는 공식은 간단하지만 효과적입니다. 다음은 사다리꼴 넓이를 계산하는 공식입니다.
넓이=2(윗변+아랫변)×높이
여기서 윗변은 사다리꼴의 윗 부분의 길이, 아랫변은 아랫 부분의 길이, 높이는 두 평행한 변 사이의 수직 거리입니다.
이 공식을 사용하면 어떤 크기의 사다리꼴이든 넓이를 효과적으로 계산할 수 있습니다.
공식 사용 예시
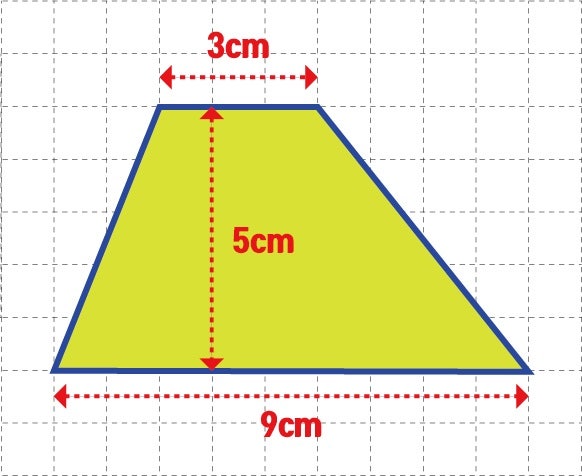
이제 공식을 어떻게 사용하는지 실제 예시를 통해 살펴보겠습니다. 예를 들어, 윗변이 5, 아랫변이 7, 높이가 4인 사다리꼴이 있다고 가정해 봅시다.
넓이=2(5+7)×4
넓이=212×4
넓이=248
넓이=24
따라서, 이 사다리꼴의 넓이는 24입니다.
FAQ
1. 사다리꼴과 평행사변형의 차이점은 무엇인가요?
사다리꼴과 평행사변형은 모두 평행한 변을 가지고 있지만, 사다리꼴은 윗변과 아랫변의 길이가 다르며, 평행사변형은 모든 변의 길이가 서로 같습니다.
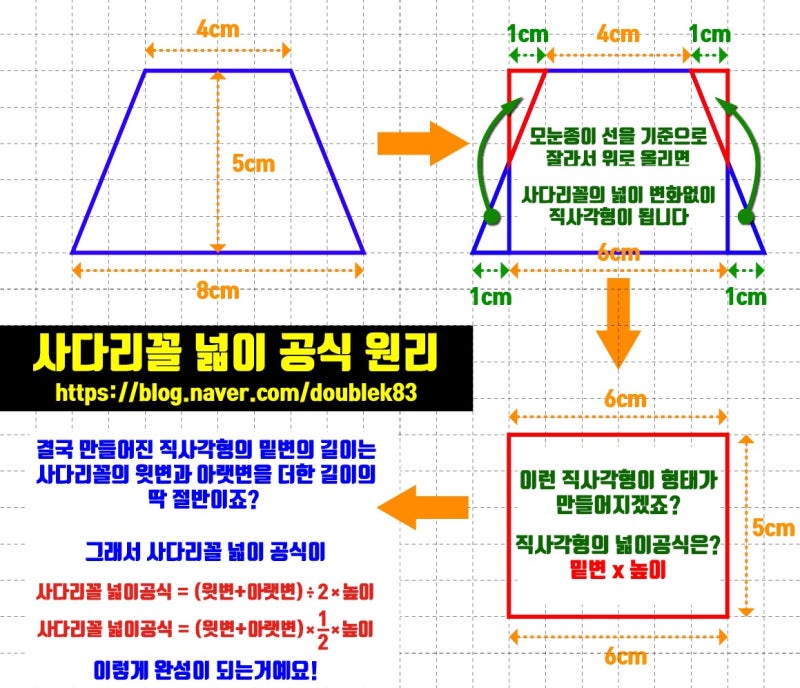
2. 왜 사다리꼴의 넓이를 계산하는 공식에 2를 곱하나요?
이는 사다리꼴이 두 개의 삼각형으로 나누어지는데, 각 삼각형의 넓이를 계산하고 합치기 위해 2로 나누는 것입니다.
3. 사다리꼴의 높이는 어떻게 정의되나요?
사다리꼴의 높이는 두 평행한 변 사이의 수직 거리를 의미합니다. 이것은 윗변과 아랫변을 연결하는 수직선을 통해 쉽게 측정할 수 있습니다.
이 가이드를 통해 사다리꼴 넓이 공식에 대한 이해를 높일 수 있었기를 바랍니다. 더 많은 예시와 문제를 풀어보며 실력을 향상시켜보세요.
상위 44 사다리꼴 둘레 공식
![닥터 Y] 사다리꼴의 넓이를 구하는 5가지 방법 : 네이버 블로그 닥터 Y] 사다리꼴의 넓이를 구하는 5가지 방법 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAxNzA2MjhfNjEg/MDAxNDk4NjIyMzM1MDE0.rfvX99RmSup7HDeYp9_pmTfMTelhWlPTRqPU3zAN-B4g.0ZUZiG5zVfxKddrDDIuxpSPA7YXnnxIjgiKzxkT7oQ4g.JPEG.naverschool/12_02.jpg?type=w800)

![중2-2] 등변사다리꼴의 둘레 📘[라이트쎈] 0377번 📘[RPM] 0344번 📘[쎈] 0385번 📘[일품] p. 25 9번 - YouTube 중2-2] 등변사다리꼴의 둘레 📘[라이트쎈] 0377번 📘[Rpm] 0344번 📘[쎈] 0385번 📘[일품] P. 25 9번 - Youtube](https://i.ytimg.com/vi/HayjZC7fC50/maxresdefault.jpg)

![닥터 Y] 사다리꼴의 넓이를 구하는 5가지 방법 : 네이버 블로그 닥터 Y] 사다리꼴의 넓이를 구하는 5가지 방법 : 네이버 블로그](https://mblogthumb-phinf.pstatic.net/MjAxNzA2MjhfMTQ5/MDAxNDk4NjIyMzM1MTE3.68r-nKJSyuUZkmh0Ikkzr1R3K3JX9zwXV3Xaf3X4brIg.tfvsQ5gwLBu542KgllaGyMUjAFSyCYFOovLuYF9kCiEg.JPEG.naverschool/12_04.jpg?type=w800)

![초등수학] 사다리꼴의 넓이 공식을 유도해 보자.|사다리꼴의 넓이 공식은 평행사변형의 넓이에서부터!! - YouTube 초등수학] 사다리꼴의 넓이 공식을 유도해 보자.|사다리꼴의 넓이 공식은 평행사변형의 넓이에서부터!! - Youtube](https://i.ytimg.com/vi/0syZHbyZ7kc/mqdefault.jpg)





![기초 수학] 직사각형 삼각형 사다리꼴 넓이 구하는 공식 - YouTube 기초 수학] 직사각형 삼각형 사다리꼴 넓이 구하는 공식 - Youtube](https://i.ytimg.com/vi/n4XpyIld4G8/maxresdefault.jpg)

![기초 수학] 직사각형 삼각형 사다리꼴 넓이 구하는 공식 - YouTube 기초 수학] 직사각형 삼각형 사다리꼴 넓이 구하는 공식 - Youtube](https://i.ytimg.com/vi/6hbyGPVLV5U/hq720.jpg?sqp=-oaymwEhCK4FEIIDSFryq4qpAxMIARUAAAAAGAElAADIQj0AgKJD&rs=AOn4CLCrN0KJ2AJvZeGzKrAtJmvhAzD5SQ)
See more here: trainghiemtienich.com
Learn more about the topic 사다리꼴 둘레 공식.